JLOG
[머신러닝/딥러닝 기초]Linear Regression과 Gradient descent algorithm 본문
[머신러닝/딥러닝 기초]Linear Regression과 Gradient descent algorithm
정정선선 2020. 9. 22. 08:57!! 목표
선형적인 관계에 있는 Linear Regression(선형회귀)와기울기를 이용해 loss를 줄이고 W,b를 갱신하는 Gradient descent algorithm(경사하강법)에 대해 알아보자
1. Linear Regression의 Hypothesis 와 cost 설명
-Linear Regresssion
Linear Regression : 선형적인 관계에 있는 식이라 생각할 수 있다.
데이터들을 바탕으로 적절한 Linear 관련 식을 찾아, Regression 할 수 있도록 한다.

-Hypothesis : 어떤 값이 나올지 예측하는 것
H(x) = Wx+b에서 정답에 제일 부합하는 W & b를 찾는 것이 목표

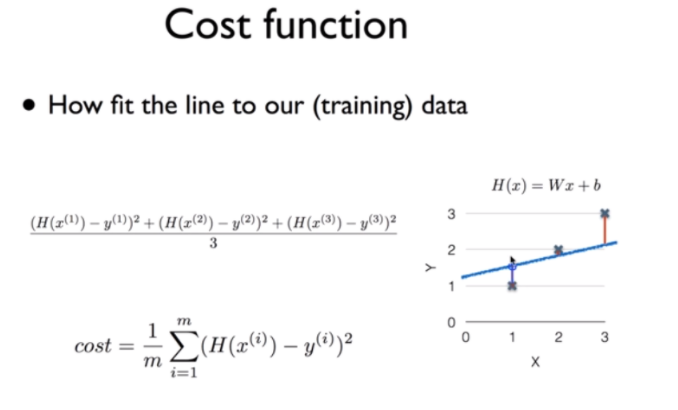
-Cost Function (Loss Function)
정해진 H(x) = Wx+b의 식에서 값들에 대한 Cost(Loss)를 계산하는 식
Cost를 최소화하도록 W, b를 조절하는 목적의 Training이 진행 된다.
예측값 H(x)과 정답(label값=y)을 빼서 제곱해주어 Cost를 구했다.
Cost는 양수, 음수가 구별되어서는 안되 제곱해주었고, 절대값을 취해주어도 된다고 한다.
만약 제곱한 경우에는 기울기가 가팔라져 Gradient descent algorithm에서 변화가 절대값을 취한 것보다 더 빨리 일어날 것을 예측할 수 있다.

-Gradient descent algorithm - Linear Regression의 cost 최소화 알고리즘의 원리 설명
수식을 간단화하기 위해 b를 무시하고 진행한다.
각 W의 값이 다를 때 마다 Cost 값이 다르게 나온다.
CostFunction에 제곱을 하는 이유는 앞서 말했듯이 모두 양수로 만들어서 미분하기 편하기 위해서 이다.
해당 Cost_function을 그래프로 그리면 아래와 같이 나타난다.
Cost를 최소화하기위해 Gradient descent algorithm을 사용한다.

-Gradient descent algorithm(경사하강법)
시작하는 지점에서 미분을 통해 경사를 구한다. 각 점에서 기울기를 이용해 가장 Cost가 최소화 되도록 이동한다.
식의 Cost 앞에 - 값은 기울기가 +면 뒤로가고, -면 앞으로 가면서 Cost가 최소화 되는 방향으로 이동한다는 의미를 가지고 있다.


여기서 식을 나타내면 Wnew = Wold - α*C'(x,y)이다.
왜 -를 해주는지는 오른쪽 그림을 보면 알 수 있다.
기울기가 + 값을 가지면 w은 왼쪽으로 이동해야지 Error를 줄일 수 있다.
이와 같이 기울기의 증가 감소와 반대로 이동해야지 기울기를 줄일 수 있기 때문이다.
-learning rate(α) : 한번 W&b 갱신하는 정도를 정할 수 있다.
각 Cost Function의 미분 값과 learning rate를 곱한 값을 이용한다.
이 gradient descent algoritm을 이용해 W를 update하면서 Cost를 최소화한다.

항상 Cost Function을 설계할때 반드시 아래 사진과 같이 Convex function의 모양이 되는지 확인해야한다.
만약 저렇게 밥그릇 모양이 아니면 경사하강법을 사용할 때 Gradient Vanshing, local minimum 같은 문제가 발생할 수 있다.
*참고
Gradient Vanshing : 기울기가 거의 0에 가까워 Cost가 최소가 아니지만 학습이 진행되지 않는 것.
local minimum : 원하는 글로벌한 최소 Cost 값이 아니라 부분적으로 Cost 최소값에 갇혀 버리는 것.
수식으로 확인할 수 없지만 다차식으로 갈수록 minmum한 값에 수렴한다고 한다.

이글은 모두를 위한 딥러닝 시즌1[Lab2, 3]을 참고해 공부용으로 정리 되었습니다.
출처
www.youtube.com/watch?v=qPMeuL2LIqY&list=PLlMkM4tgfjnLSOjrEJN31gZATbcj_MpUm&index=2
'AI > basic concepts of AI' 카테고리의 다른 글
| Loss Function 정리(MSE, Cross Entropy error) (0) | 2021.03.09 |
|---|---|
| [딥러닝 기초]Momentum 설명 (0) | 2021.03.09 |
| [머신러닝/딥러닝 기초] 기본적인 Machine Learning의 용어와 개념 (0) | 2020.09.08 |

